complex to measure the shape of the universe. In fact, this question has a very counterintuitive answer, because when we think of the shape of something, we might imagine an object seen from its exterior.
We should not think of the universe in the same way. The universe doesn't have an outer perimeter, and nothing exists outside it, because there isn't an outside.
As an analogy, consider the shape of our galaxy, the Milky Way. We can infer that it is a spiral based on maps of the stars in its spiral arms, but we cannot go outside the galaxy to see this spiral structure firsthand. However, with telescopes, we can see other spiral galaxies from the outside and conclude that the Milky Way is like them. Where this analogy breaks down, however, is that we cannot step outside the universe because there is no outside to step into.
By definition, the universe is everything in existence, so nothing can exist outside it. That said, modern theories such as chaotic inflation, brane theory and parallel realities have blurred that definition.
We'll address those ambiguities later. For the time being, when we think about shape, we're referring to the geometry of space. For example, on a flat surface, the angles of a triangle always add up to 180 degrees, but on a curved surface, they can add up to more or less than 180 degrees. On a flat surface, parallel lines remain parallel for as long as they extend, but on a curved surface, they can converge or diverge, or cross over. If you begin moving in one direction, do you continue moving away from where you began, or do you loop back on yourself? These are the questions we're talking about when we refer to the geometry of the universe.
Shape of the universe FAQs
How do scientists know the shape of the universe?
We measure the geometry of the universe by measuring the average density of matter in space and comparing it to a critical density, which dictates the curvature of space.
What shapes the universe?
The gravitational effect of matter can affect the curvature of space, per general relativity, but quantum effects during the Big Bang also influenced the shape of the universe.
Is the universe a sphere or flat?
Whether the universe is flat or curved like a sphere (closed) depends on how close the density of matter is to the critical density. Measurements show that the density is almost a match for the critical density, which indicates a flat universe.
What is the true shape of the universe?
A flat universe has Euclidean geometry, and the simplest shape it can adopt is that of a sheet. There are also other, more complex shapes that a flat universe could have, such as a "3-torus."
How to measure the shape of the universe
The geometry of the universe is determined by the density of matter within the universe. Albert Einstein's theory of general relativity describes how matter can curve space, so the matter's density can control the curvature and geometry of space on the largest scales.
The key value is the "critical density," which is denoted by the Greek letter omega (𝛀). The universe has the critical density if it contains, on average, six hydrogen atoms per cubic meter. But matter is not spread evenly throughout the universe. We know this because we see it concentrated within galaxies and absent in the gaps between galaxies. However, when we talk about the density of matter in the universe, we're imagining spreading every atom in the universe (three-quarters of which are hydrogen) evenly across space.
There's also dark matter, which we can infer only from its gravitational effects, but we know it must account for about 85% of all matter in the universe. Having a handle on the amount of dark matter in the universe is crucial for figuring out its geometry and its fate.
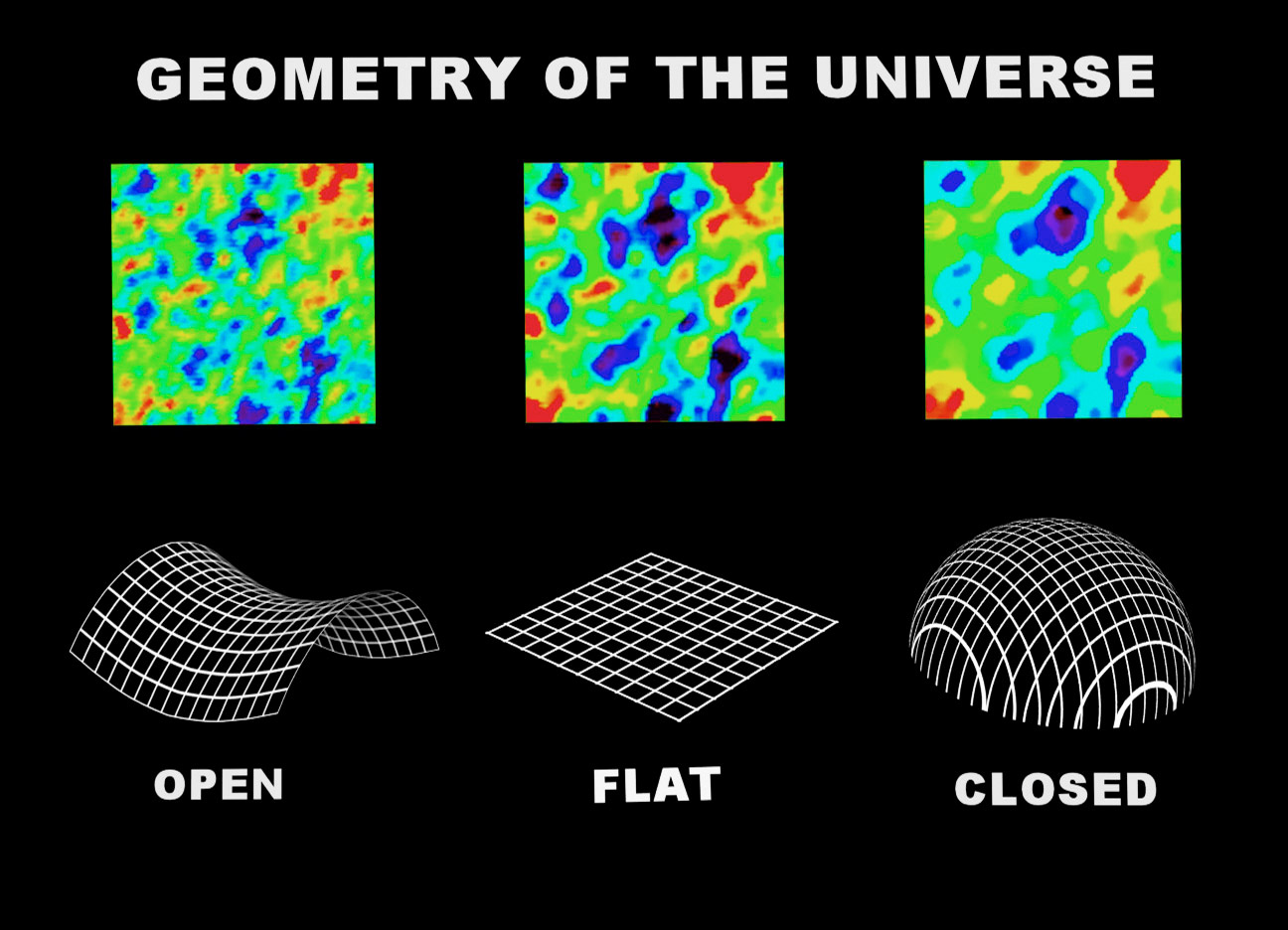
Let's explore three possibilities for the geometry of the universe: open, closed or flat. If the density of matter in the universe is greater than the critical density, then we say our universe is closed and has a positive curvature. In a closed universe, you could set out on a journey across space, traveling in a straight line, and you'd eventually loop around and arrive back at your starting point. The positive curvature is convex rather than concave, and it would imply a universe shaped like the surface of a sphere. In a sphere, two parallel lines would not remain parallel forever; first they would diverge, and then they would converge back onto their point of origin and cross over each other.
If the density of matter in the universe is less than the critical density, the geometry of the universe is described as being open and negatively curved, like the concave shape of a saddle, and quite possibly infinite in extent.
But if the universe is keenly balanced so that the density of matter is equal to the critical density, then the geometry of the universe is described as being flat. A flat geometry is a Euclidean geometry, named after the ancient Greek mathematician Euclid, wherein parallel lines remain parallel and the angles of a triangle add up to 180 degrees.
So which is it? NASA's Wilkinson Microwave Anisotropy Probe (WMAP) and the European Space Agency's Planck mission have measured the matter-energy density of the universe, and both have found omega to be equal to the critical density. In other words, the universe seems to have a flat geometry.
What are some possible shapes of our universe?
WMAP and Planck measured omega with a great deal of precision, and cosmologists are very confident that the universe is flat. This prediction, as we've seen, is dictated by the critical density and general relativity.
However, an international team called the Collaboration for Observations, Models and Predictions of Anomalies and Cosmic Topology (COMPACT) found that a flat universe does not necessarily rule out complicated shapes. In their research paper, they focused on a shape known as a 3-torus.
A one-dimensional circle is known as a 1-torus. A 2-torus, which is in two dimensions, is a doughnut shape. Now imagine a 3-torus, which is in three dimensions. Picture a cube turned inside out, with opposite sides bending and warping until they face each other and touch. This is a 3-torus. There are three types: this basic example, and then one twisted by 90 degrees and another twisted by 180 degrees. The family of 3-torus shapes can maintain the impression of a flat, Euclidean geometry, according to the COMPACT team.
A 3-torus or some other, exotic shape could, in theory, result from quantum effects that took place during the Big Bang and shaped how the universe subsequently unfolded. So how would we know if we lived inside a 3-torus universe? The way space bends back on itself would mean that we would see repeat images of the same part of the universe in different parts of the sky as the light traveled along the different paths of this complex loop. It would be like living in a cosmic hall of mirrors. All we'd need to do is identify these repeated images.
The COMPACT team has studied the cosmic microwave background (CMB) — the radiation left over from the Big Bang — looking for any patterns. They haven't found any, but there are two caveats. One is that the scale of the 3-torus could be so large that light traveling around one of its loops hasn't had time to reach us yet. The other is that although the standard 3-torus is ruled out if the length scale is small enough, the 90- and 180-degree twisted versions haven't been ruled out yet. That's because they twist the repeated images, making them more complicated to identify, and a comprehensive search for such twisted repeat patterns in the CMB hasn't been performed yet.
Even if all of the 3-torus shapes are ruled out, there are 18 mathematically possible shapes that are consistent with a flat universe, and perhaps one of them is the true shape of our universe, the COMPACT team said.
The universe's shape in multidimensional space
According to some theories — for which we don't have any hard evidence for — there is something outside our universe. This something is a multidimensional hyperspace, sometimes called "the bulk."
Within the bulk, as the theory goes, exists our four-dimensional universe (three physical dimensions, plus time), sitting on a membrane ("brane") within the bulk's higher-dimensional space. The number of dimensions in the bulk varies depending on the model — some say five, others seven, others many more. Regardless, our universe would then adopt the shape of this brane as seen from within the bulk. There could be other branes in the bulk too, each with their own independent universes. Sometimes those branes could collide, instigating a new Big Bang. This cyclic model of branes colliding is called the ekpyrotic theory.
Another model is that of chaotic, or eternal, inflation, which expands upon Alan Guth's theory of inflation from the early 1980s. Inflation was introduced to explain why different parts of the universe appear similar even though they are too far apart for any causal connection — that is, there has not been enough time for light and information to travel between these areas. Inflation suggests that at the moment of the Big Bang, these areas were close enough to share properties, and then an incredibly brief but powerful burst of inflation expanded the fledgling universe fast enough to separate these areas.
Chaotic inflation is designed to solve certain problems with Guth's original model of inflation, but it implies that different parts of inflationary space stop inflating at different periods, and these parts effectively bud off to form their own pocket universes, each with their own properties, curvatures and shapes.
Fate of the universe
he geometry of space will also determine the ultimate fate of the universe.
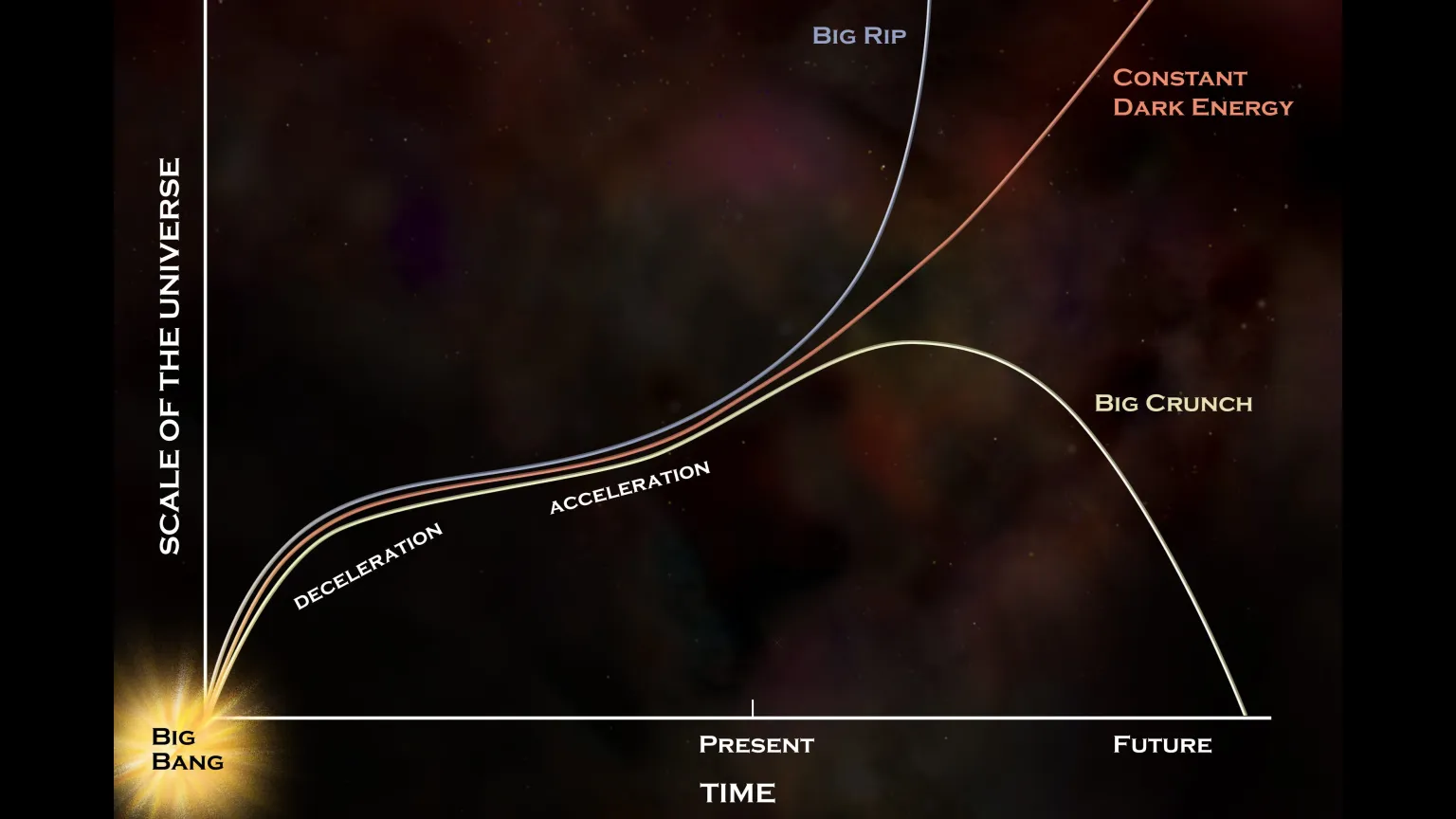
In a closed universe, where the density of matter is high enough to exceed the critical density, gravity will eventually halt cosmic expansion. Instead, the universe will begin to contract, like rewinding the clock, and shrink until it comes together in a single point referred to as the "Big Crunch," which would be the mirror image of the Big Bang.
In an open universe, where the density of matter is less than the critical density, there isn't enough gravity to slow the expansion of the universe. Powered by dark energy, the expansion continues to accelerate until the "Big Rip," when even space is torn apart.
But in a flat universe, the cosmos would expand forever but gradually slow, thus avoiding a Big Rip and not collapsing in a Big Crunch. However, this would result in the "Big Freeze," with energy being so spread out and the universe reaching a state of maximum entropy, meaning that no work can be done and no energy can be transferred because everywhere would have exactly the same, cold temperature.
The big caveat to all of this is dark energy, which is currently accelerating the expansion of space. Dark energy might be the cosmological constant — a latest energy of space that always has the same strength. Or it could be an energy field that pervades the entire universe but can fluctuate in strength at different points in time and space. Because we don't know for sure how dark energy will behave in the future, we're also uncertain about the fate of the cosmos.
Additional resources
A flat universe has Euclidean geometry, which is named after the ancient Greek mathematician Euclid. This essay by Benjamin Wardhaugh digs into the identity of the famed mathematician.
ESA's Planck mission has observed the cosmic microwave background radiation and, from that, deduced the amount of matter and dark matter in the universe, the density of matter in the cosmos, and the ways those measurements affect the geometry of the universe.
Neil deGrasse Tyson discusses the shape of the universe in an episode of "Star Talk."
Bibliography
Christopher S. Baird, 'Where is the Edge of the Universe?', West Texas A&M University, (2016) https://www.wtamu.edu/~cbaird/sq/2016/01/20/where-is-the-edge-of-the-universe/
Andrei D. Linde, 'Chaotic Inflation', Physics Letters B, Vol 129, issues 3–4 (1983) https://www.sciencedirect.com/science/article/abs/pii/0370269383908377
Roland Pease, 'Brane New World', Nature, 411 (2001) https://www.nature.com/articles/35082684
'Critical Density', Swinburne Encyclopedia of Astronomy, https://www.astronomy.swin.edu.au/cosmos/C/Critical+Density
ESA, 'History of Cosmic Structure Formation', https://www.esa.int/Science_Exploration/Space_Science/Planck/History_of_cosmic_structure_formation
'Astronomers Observe the Effect of Dark Matter on the Evolution of the Galaxies', Instituto de Astrofísica de Canarias (2024) https://www.iac.es/en/outreach/news/astronomers-observe-effect-dark-matter-evolution-galaxies
NASA, 'Universe 101: Will the Universe Expand Forever?' (2024), https://wmap.gsfc.nasa.gov/universe/uni_shape.html
J. Schombe, 'Geometry of the Universe', University of Oregon, https://pages.uoregon.edu/jschombe/cosmo/lectures/lec15.html
C. L. Bennett et al, 'First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results', The Astrophysical Journal Supplement Series, Vol 148, No. 1 (2003) https://iopscience.iop.org/article/10.1086/377253
Planck Collaboration, 'Planck 2018 results VI: Cosmological Parameters', Astronomy & Astrophysics, 641, A6, (2020) https://www.aanda.org/articles/aa/full_html/2020/09/aa33910-18/aa33910-18.html
Yashar Akrami et al, 'Promise of Future Searches for Cosmic Topology', Physical Review Letters, 132 (2024) https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.171501
'Torus', Wolfram MathWorld, https://mathworld.wolfram.com/Torus.html
Zeeya Merali, 'Doughnut-Shaped Universe Bites Back', Nature (2008), https://www.nature.com/articles/news.2008.854
Marc Lacièze-Rey and Jean-Pierre Luminet, 'Cosmic Topology', Physics Reports, Vol 254, Issue 3, (1995) https://www.sciencedirect.com/science/article/abs/pii/037015739400085H?via%3Dihub
Neil J. Cornish et al, 'Constraining the Topology of the Universe', Physical Review Letters, 92 (2004) https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.92.201302
Johannes R. Eskilt, 'Cosmic Topology, Part IIa: Eigenmodes, Correlation Matrices and Detectability of Orientable Euclidean Manifolds', Journal of Cosmology and Astroparticle Physics, Vol 2024 (2024), https://iopscience.iop.org/article/10.1088/1475-7516/2024/03/036
Alan Guth, 'Inflation', Carnegie Observatories Astrophysics Series, Vol 2: Measuring and Modeling the Universe (2004) https://sites.astro.caltech.edu/~ccs/Ay21/guth_inflation.pdf
Jean-Luc Lehners, 'Ekpyrotic and Cyclic Cosmology', Physics Reports, Vol 465, issue 6 (2008) https://www.sciencedirect.com/science/article/abs/pii/S0370157308001877
Saul Perlmutter, 'Supernovae, Dark Energy and the Accelerating Universe', Physics Today, Vol 56, Issue 4 (2003) https://pubs.aip.org/physicstoday/article/56/4/53/923992/Supernovae-Dark-Energy-and-the-Accelerating
'Will the Universe Last Forever?' CSIRO Parkes Observatory, https://www.parkes.atnf.csiro.au/people/sar049/eternal_life/universe/universe.html
Robert Caldwell and Marc Kamionkowski, 'The Physics of Cosmic Acceleration' Annual Review of Nuclear and Particle Science, Vol 59 (2009) https://www.annualreviews.org/content/journals/10.1146/annurev-nucl-010709-151330
Yun Wang et al, 'Current Observational Constraints on Cosmic Doomsday', Journal of Cosmology and Astroparticle Physics, Vol 2004 (2004) https://iopscience.iop.org/article/10.1088/1475-7516/2004/12/006
R. R. Caldwell, Rahul Dave, Paul J. Steinhardt, 'Cosmological Imprint of an Energy Component with General Equation of State', Physical Review Letters, Vol 80, No 1582 (1998) https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.80.1582
Join our Space Forums to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at: community@space.com.
